Applications of the Fourier Transform in Electrical Circuits

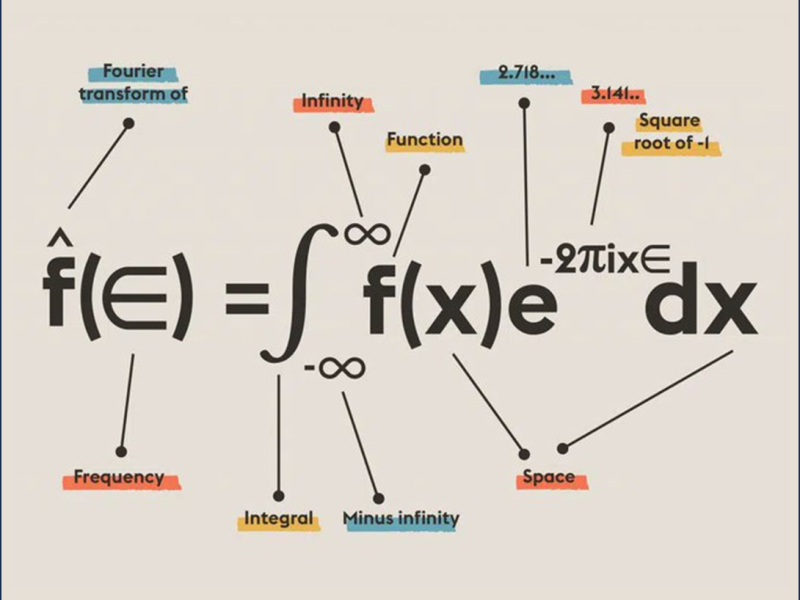
Abstract: This diploma thesis explores the application of series and Fourier transforms to the study of electrical circuits, with a particular focus on their role in the operation of internal combustion engines. By leveraging mathematical techniques such as Fourier transforms, the thesis provides insights into how electrical circuits can be modeled and analyzed to improve the efficiency and performance of engine systems. The research contributes to the development of a mathematical framework that aids in the optimization of electrical circuits in automotive engineering.

Introduction: In the realm of automotive engineering, internal combustion engines rely heavily on the precise functioning of electrical circuits. These circuits govern various engine components, impacting the overall performance and efficiency of the vehicle. This thesis proposes the use of series and Fourier transforms as key tools for analyzing electrical circuits in internal combustion engines, offering a mathematical approach to solving complex problems in circuit design and functionality.

Objectives:

• Utilize series and Fourier transforms to develop a comprehensive understanding of electrical circuits used in internal combustion engines.
• Analyze the dynamic behavior of these circuits through the lens of mathematical models, exploring how Fourier transforms can enhance the design and efficiency of engine-related electrical systems.
• Investigate the practical applications of mathematical analysis in optimizing the performance of electrical circuits within internal combustion engines.
• Provide a robust mathematical framework for the study of electrical circuits that can be applied to various automotive engineering challenges.

Methodology: The methodology encompasses the following stages:

• Mathematical Modeling: Utilize series and Fourier transforms to construct models representing the behavior of electrical circuits in internal combustion engines.
• Analysis and Simulation: Apply mathematical tools to simulate the operation of these circuits, exploring how different variables affect their performance.
• Application to Engineering Systems: Evaluate the real-world applicability of these models in the design and optimization of electrical circuits for internal combustion engines.
• Validation: Test the models against actual engine circuit designs, validating their effectiveness in predicting circuit performance and offering improvements.

Expected Contributions:

• Development of a mathematical model using Fourier transforms that improves the understanding of electrical circuits in internal combustion engines.
• Insights into the use of advanced mathematical techniques in automotive engineering, demonstrating their potential to enhance engine performance through better circuit design.
• A framework that allows for the integration of complex mathematical concepts into practical engineering applications, paving the way for further research in the field.

Prerequisite knowledge: Mathematical Analysis, Linear Algebra, Nonlinear Differential Equations, Bifurcation Theory, Complexity Theory.

Conclusion: This thesis aims to bridge the gap between mathematical theory and engineering practice by applying series and Fourier transforms to the study of electrical circuits in internal combustion engines. Through rigorous mathematical analysis, the work seeks to optimize circuit performance, offering valuable insights for future innovations in automotive engineering.