Stability Study of Autonomous Systems Using Complexities

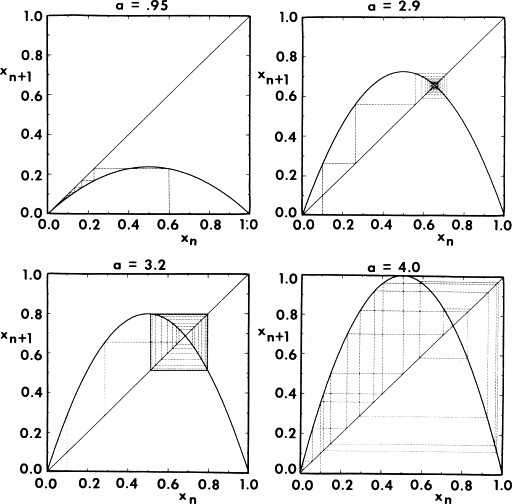
Abstract: This diploma thesis investigates the stability of Autonomous Nonlinear Systems using Central Multiplicity Theory. The focus is placed on analyzing the equilibrium points of such systems, determining their stability and behavior. By employing advanced mathematical tools, the thesis provides a deeper understanding of how equilibrium points behave in nonlinear dynamics, contributing to the broader field of system stability and control theory.

 Introduction: Autonomous Nonlinear Systems play a crucial role in various scientific and engineering applications, where stability is of paramount importance. These systems exhibit complex behavior due to their nonlinear nature, making their stability analysis challenging. This thesis proposes the use of Central Multiplicity Theory as a mathematical framework to study the equilibrium points of Autonomous Nonlinear Systems, providing insights into their stability characteristics and bifurcation behavior.

 Objectives:

• Apply Central Multiplicity Theory to analyze the equilibrium points of Autonomous Nonlinear Systems.
• Investigate the stability of these systems by exploring the relationship between equilibrium points and system dynamics.
• Develop a mathematical framework that utilizes Central Multiplicity Theory for studying nonlinear differential equations and their impact on system stability.
• Examine how bifurcation theory and complexity theory can be integrated into the stability analysis of nonlinear systems.

Methodology: The methodology comprises several key stages:

• Mathematical Formulation: Use Central Multiplicity Theory to construct mathematical models representing Autonomous Nonlinear Systems.
• Equilibrium Point Analysis: Identify and analyze the equilibrium points of the systems, determining their stability through mathematical techniques such as bifurcation theory.
• Stability Analysis: Apply Central Multiplicity Theory to assess the stability of the identified equilibrium points, investigating how system parameters influence their behavior.
• System Simulation: Implement simulations of Autonomous Nonlinear Systems to validate theoretical findings, exploring real-world applications of the stability analysis framework.

 Expected Contributions:

• A detailed analysis of the stability of Autonomous Nonlinear Systems using Central Multiplicity Theory, offering new insights into the behavior of equilibrium points.
• A mathematical framework for stability analysis that can be applied to a wide range of nonlinear systems in engineering and scientific research.
• Enhanced understanding of the role of bifurcation and complexity theory in determining system stability, paving the way for further research into nonlinear dynamics.

Prerequisite knowledge: Mathematical Analysis, Linear Algebra, Nonlinear Differential Equations, Bifurcation Theory, Complexity Theory.

 Conclusion: This thesis aims to advance the study of Autonomous Nonlinear Systems by applying Central Multiplicity Theory to analyze their stability. By focusing on the equilibrium points, the research seeks to provide a robust mathematical framework that can be used to predict and control system behavior in various practical applications. The work highlights the importance of stability analysis in nonlinear systems, contributing valuable insights to the field of dynamical systems and control theory.